สมการเชิง เส้น 1 ตัวแปร
กฤษณ์ ท. ผู้เชี่ยวชาญ AI

การแก้อสมการ
เชิงเส้นตัวแปรเดียว
เนื้อหา
ในภาคเรียนนี้
A Course Syllabus

สมการเชิงเส้นตัวแปรเดียว
แยก ตปก. พหุนามดีกรีสูงกว่า 2
สมการกำลังสองตัวแปรเดียว
ความคล้าย
กราฟของฟังก์ชั่นกำลัง 2
สถิติ (3)


การแก้อสมการเชิงเส้นตัวแปรเดียว

การหาคำตอบทั้งหมดของอสมการ

ใช้การแทนค่า หรือ

สมบัติการบวกของการไม่เท่ากัน
(Additive property of inequality)

สมบัติการคูณของการไม่เท่ากัน
(Multiplicative property of inequality)

* ปรับแต่งอสมการอย่างไรก็ได้ ให้ยังคงความสมมูลกัน (Equivalent)

สมบัติการบวกของการไม่เท่ากัน
ให้ a, b, และ c แทนจำนวนจริงใด ๆ
<
ถ้า
แล้ว
<
\leqslant
ถ้า
แล้ว
a
b
a + c
b + c
a
b
a + c
b + c
\leqslant
ให้ a, b, และ c แทนจำนวนจริงใด ๆ
>
ถ้า
แล้ว
>
\geqslant
ถ้า
แล้ว
a
b
a + c
b + c
a
b
a + c
b + c
\geqslant

ตัวอย่าง
-4<0
ถ้า
แล้ว
<
-4 + 8
0 + 8
จะได้
4<8
x-6<10
ถ้า
แล้ว
<
(x-6) + 6
10 + 6
จะได้
x<16
x-21\geqslant 32
ถ้า
แล้ว
\geqslant
(x-21) + 21
32 + 21
จะได้
x\geqslant 53

สมบัติการคูณของการไม่เท่ากัน
ให้ a, b, และ c เป็นบวก ( + )
<
ถ้า
แล้ว
<
\leqslant
ถ้า
แล้ว
a
b
ac
bc
a
b
ac
bc
\leqslant
ให้ a, b, และ c เป็นลบ ( - )
<
ถ้า
แล้ว
>
\leqslant
ถ้า
แล้ว
a
b
ac
bc
a
b
ac
bc
\geqslant

สมบัติการคูณของการไม่เท่ากัน
ให้ a, b, และ c เป็นบวก ( + )
>
ถ้า
แล้ว
>
\geqslant
ถ้า
แล้ว
a
b
ac
bc
a
b
ac
bc
\geqslant
ให้ a, b, และ c เป็นลบ ( - )
>
ถ้า
แล้ว
<
\geqslant
ถ้า
แล้ว
a
b
ac
bc
a
b
ac
bc
\leqslant

ตัวอย่าง
8<11
ถ้า
แล้ว
<
8 x 3
11 x 3
จะได้
24<33
7<15
ถ้า
แล้ว
>
7 x -2
15 x -2
จะได้
-14>-30
x\leqslant 20
ถ้า
แล้ว
\leqslant
(x) x 4
20 x 4
จะได้
4x\leqslant 80

จงแก้อสมการต่อไปนี้
2x-4>8
3x-6\leqslant5x+8
2(x-15)\leqslant3x+5
5x-3\geqslant \frac{1}{3} x+2
5x-3\geqslant \frac{1}{3} x+2
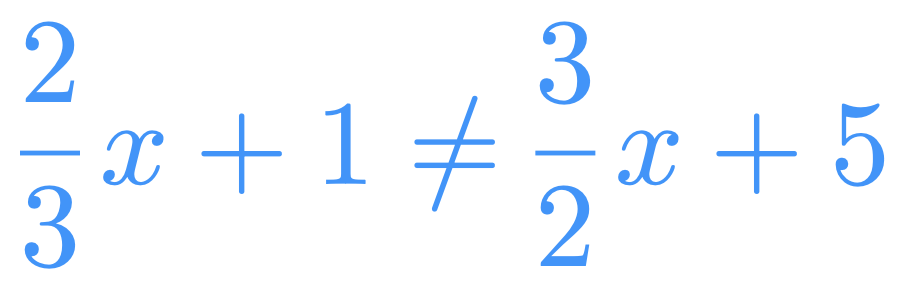

โจทย์ปัญหาเกี่ยวกับอสมการเชิงเส้นตัวแปรเดียว
-
ขั้นที่ 1 วิเคราะห์โจทย์ เพื่อดูว่า
โจทย์กำหนดอะไรมาให้ ? และให้หาอะไร ? -
ขั้นที่ 2 กำหนดตัวแปรแทนสิ่งที่โจทย์ให้หา
-
ขั้นที่ 3 เขียนอสมการตามเงื่อนไขในโจทย์
-
ขั้นที่ 4 แก้อสมการเพื่อหาคำตอบ
-
ขั้นที่ 5 ตรวจสอบคำตอบที่ได้กับเงื่อนไขของโจทย์

จงแก้โจทย์ปัญหาต่อไปนี้
ต้นกล้าต้องการทำรั้วล้อมรอบสนามรูปสี่เหลี่ยมผืนผ้าแห่งหนึ่งซึ่งมีด้านยาวยาวกว่าด้านกว้าง 8 เมตร ความยาวโดยรอบสนามไม่เกิน 204 เมตร จงหาความยาวของด้านกว้างของสนามแห่งนี้

จงแก้โจทย์ปัญหาต่อไปนี้
ผลบวกของจำนวนคี่สามจำนวนเรียงกันมีค่าน้อยกว่า 81 จำนวนคี่ทั้งสามนั้นจำนวนที่มากที่สุดที่เป็นไปได้คือจำนวนใด
© Aj. Krit Th.
https://www.kritth.com