ระบบจำนวนจริง
กฤษณ์ ท. ผู้เชี่ยวชาญ AI

อตรรกยะ
รากที่ 2 & 3
เนื้อหา
ในภาคเรียนนี้
A Course Syllabus

ทฤษฎีบทพีทาโกรัส
ความรู้เบื้องต้นเกี่ยวกับจำนวนจริง
ปริซึมและทรงกระบอก
การแปลงทางเรขาคณิต
สมบัติของเลขยกกำลัง
พหุนาม


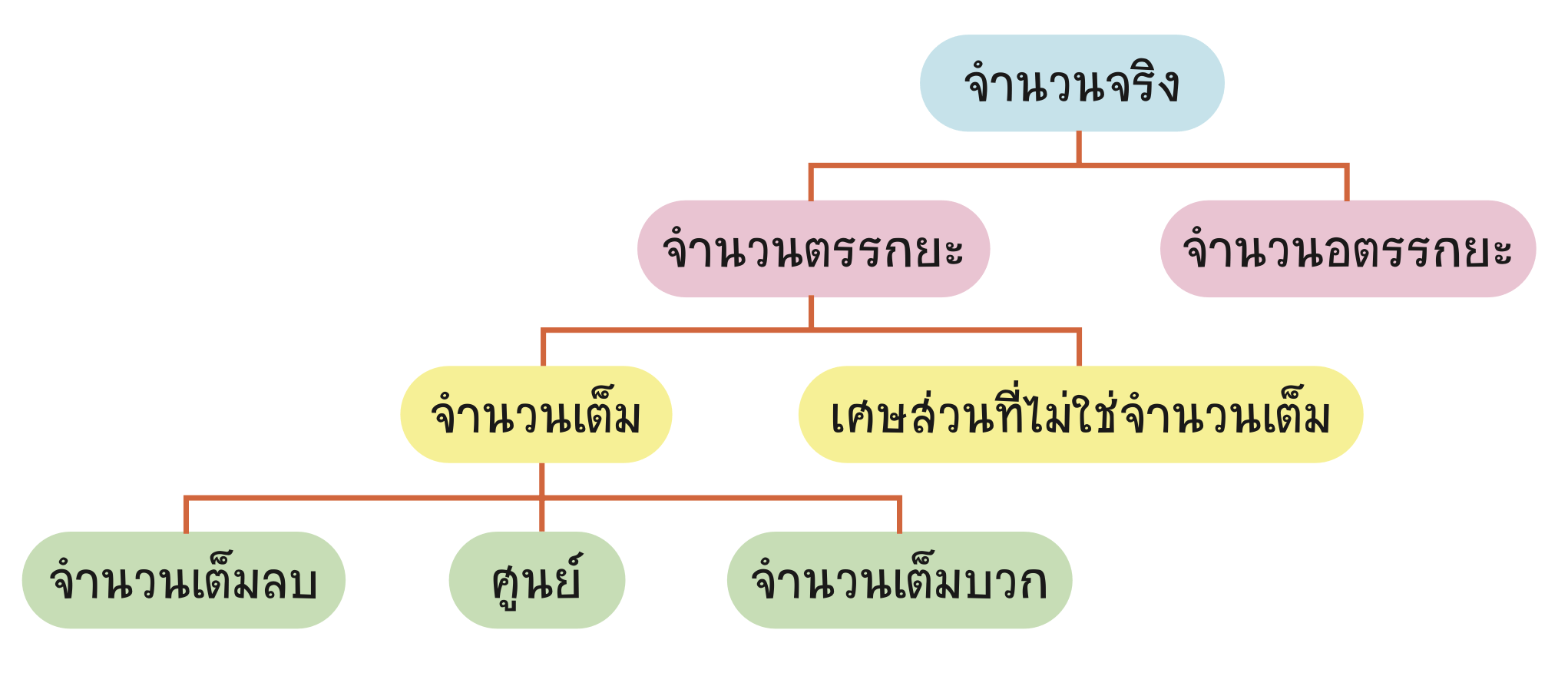


จำนวนอตรรกยะ (Irrational Number)
-
ไม่สามารถเขียนเป็นเศษส่วนได้
-
ทศนิยมไม่สิ้นสุดและไม่ซ้ำ
-
จำนวนจริงที่ไม่อยู่ในจำนวนตรรกยะ
ยกตัวอย่าง เช่น
\pi ,e,\sqrt{2} ,\sqrt{3}
\sqrt{2} =1.414213562373095
\sqrt{3} =1.73205081

รากที่สอง
บทนิยาม ให้ a แทนจำนวนจริงบวกใด ๆ หรือศูนย์ รากที่สอง (square root) ของ a คือ จำนวนจริงที่ยกกำลังสองแล้วได้ a
ยกตัวอย่าง เช่น
9 เป็นรากที่สองของ 81 เนื่องจาก
9^{2}=81
−9 เป็นรากที่สองของ 81 เนื่องจาก
(-9)^2 = 81

รากที่สอง (ต่อ)
กรณฑ์ที่สองของ a

\sqrt{a}
เรียกอีกอย่างว่า
จากบทนิยามจะได้ว่า

(\sqrt{a} )^{2}=a\ \text{และ} \ (-\sqrt{a} )^{2}=a
ถ้า a = 0 รากที่สองของ a คือ 0

ถ้า a เป็นจำนวนจริงบวก รากที่สองของ a มีสองราก คือ รากที่สองที่เป็นบวก ซึ่งแทนด้วยสัญลักษณ์ และรากที่สองที่เป็นลบ ซึ่งแทนด้วยสัญลักษณ์

-\sqrt{a}
\sqrt{a}

ลองทำดู
-\sqrt{196}
จงหา. . .
\sqrt{\left( {}-37 \right)^{2}}
\sqrt{0.0225}
จงหารากที่สองของจำนวนต่อไปนี้
1,296
256
841
5.29
\frac{4}{9}
10.24
900
784
5,041
0.49
1,369
13.69
225
0.0025
36
0.0081

ลองทำดู
6\sqrt{5} \ \ \ \frac{1}{\sqrt{5}} \ \ \ \ \ \sqrt{600} \ \ \ \ \ 6.\dot{5}
จงเรียงลำดับจำนวนต่อไปนี้ จากน้อยไปมาก
-70\ \ \ \ \ -\frac{1}{64} \ \ \ \ \ -8.8\ \ \ \ \ -5\sqrt{3}
\sqrt{6} \ \ \ \ \ 7\sqrt{11} \ \ \ \ \ 5\sqrt{6} \ \ \ \ \ 2\sqrt{3}
3\ \ \ \ \ \sqrt{7} \ \ \ \ \ 2\sqrt{5} \ \ \ \ \ 3\sqrt{6}

ลองทำดู
x^{2}=961
จงหาคำตอบของสมการต่อไปนี้
x^{2}=0.0025
x^{2}=2.6569
x^{2}=\frac{2}{7}
x^{2}-67=-3
\sqrt{x} =\sqrt{0.38}

การหารากที่สอง
วิธีแยกตัวประกอบ
จงหารากที่สองของ 676
676=2\times 2\times 13\times 13
=\left( 2\times 13 \right)^{2}
=26^{2}
676=\left( -26 \right)^{2}
เนื่องจาก
และ
ดังนั้นรากที่สองของ 676 คือ 26 และ -26

ลองทำดู
-\sqrt{1,225}
จงหารากที่สองต่อไปนี้
\sqrt{2,209}

การหารากที่สอง
วิธีประมาณค่า
จงหารากที่สองของ (ทศนิยม 2 จุด)
\sqrt{7}
n
\sqrt{n}
n
n
2
4
2
7
3
9
\sqrt{7}
จะเห็นว่า 7 มีค่าใกล้เคียง 9 มากกว่า 4
ดังนั้นการประมาณค่าครั้งต่อไปสำหรับทศนิยม 1 ตำแหน่ง จึงเลือกตัวเลขระหว่าง 2.5 ถึง 2.7 (ต้องไม่เกิน 3)

จงหารากที่สองของ (ต่อ)
\sqrt{7}
n
\sqrt{n}
n
n
2.5
6.25
2
7.00
2.7
7.29
\sqrt{7}
2.6
6.76
0.24
0.29
จะเห็นว่า 7 มีค่าใกล้เคียง 6.76 มากกว่า 7.29 ดังนั้นจึงเลือก 2.6
ถ้าต้องการประมาณค่าครั้งต่อไปสำหรับทศนิยม 2 ตำแหน่ง จึงเลือกตัวเลขระหว่าง 2.60 ถึง 2.65

จงหารากที่สองของ (ต่อ)
\sqrt{7}
n
\sqrt{n}
n
n
2.60
xx
2
7.00
2.65
7.0225
\sqrt{7}
2.61
xx
2.62
xx
2.63
xx
2.64
6.9696
0.0225
0.0304
จะเห็นว่า 7 มีค่าใกล้เคียง 7.0225 มากกว่า 6.9696 ดังนั้นจึงเลือก 2.65 เป็นคำตอบของรากที่สองของ
\sqrt{7}

รากที่สองกับการเปรียบเทียบ (อสมการ)
เมื่อ a > 0, b > 0 ถ้า แล้ว
\sqrt{a} <\sqrt{b}
a < b
นอกจากนี้ยังมีสมบัติของกรณฑ์ที่สองที่ควรทราบดังนี้
เมื่อ a > 0, b > 0
\frac{\sqrt{a}}{\sqrt{b}} =\sqrt{\frac{a}{b}}
\sqrt{a} \sqrt{b} =\sqrt{ab}



ลองทำดู
แจกันทรงกระบอกใบหนึ่งมีปริมาตรประมาณ 192.5 ลูกบาศก์เซนติเมตร แจกันใบนี้มีความสูง 5 เซนติเมตร และสูตรการหาปริมาตรของทรงกระบอกเท่ากับ เมื่อ r แทนความยาวของรัศมี และ h แทนความสูง จงหาว่าแจกันใบนี้มีรัศมียาวกี่เซนติเมตร (กำหนด )
\pi r^{2}h
\pi \approx \frac{22}{7}
\frac{\sqrt{242}}{\sqrt{18}}
จงหาผลลัพธ์
7\sqrt{3} \ \ \text{และ} \ \ \ 5\sqrt{5}
จำนวนใดมีค่ามากกว่ากัน

รากที่สาม
บทนิยาม ให้ a แทนจำนวนจริงใด ๆ
รากที่สาม (cube root) ของ a คือจำนวนจริงที่ยกกำลังสามแล้วได้ a
สัญลักษณ์ อ่านว่า รากที่สามของ a (หรือ กรณฑ์ที่สามของ a)
จากบทนิยามจะได้
2 เป็นรากที่สามของ 8 เนื่องจาก
\sqrt[3]{a}
(\sqrt[3]{a} )^{3}=a
2^{3}=8
−7 เป็นรากที่สามของ −343 เนื่องจาก
(-7)^{3}=-343
ยกตัวอย่าง เช่น

พิจารณาว่าเป็นอตรรกยะ ?
-
ถ้าสามารถหาจำนวนตรรกยะที่ยกกำลังสามแล้วเท่ากับจำนวนตรรกยะที่กำหนดให้ (พอดีเป๊ะ) รากที่สามของจำนวนนั้นจะเป็นจำนวนตรรกยะ
-
ถ้าไม่สามารถหาจำนวนตรรกยะที่ยกกำลังสามแล้วเท่ากับจำนวนตรรกยะที่กำหนดให้ (พอดีเป๊ะ) รากที่สามของจำนวนนั้นจะเป็นจำนวนอตรรกยะ

ตัวอย่าง
จงหารากที่สามของ -1,000
-1,000=\left( -10 \right) \times \left( -10 \right) \times \left( -10 \right)
=\left( -10 \right)^{3}
ดังนั้น รากที่สามของ -1,000
คือ -10

ตัวอย่าง
จงหา
\sqrt[3]{\frac{64}{125}} =\sqrt[3]{\frac{4\times 4\times 4}{5\times 5\times 5}} =\sqrt[3]{\frac{4}{5} \times \frac{4}{5} \times \frac{4}{5}} =\sqrt[3]{\left( \frac{4}{5} \right)^{3}} =\frac{4}{5}
ดังนั้น คือ
\sqrt[3]{\frac{64}{125}}
\sqrt[3]{\frac{64}{125}}
\frac{4}{5}

การหารากที่สาม
วิธีแยกตัวประกอบ
จงหา
\sqrt[3]{216} =\sqrt[3]{2\times 2\times 2\times 3\times 3\times 3}
=\sqrt[3]{\left( 2\times 3 \right) \times \left( 2\times 3 \right) \times \left( 2\times 3 \right)}
ดังนั้น คือ 6
\sqrt[3]{216}
=\sqrt[3]{\left( 2\times 3 \right)^{3}} =\sqrt[3]{6^{3}} =6
\sqrt[3]{216}

รากที่สามกับการเปรียบเทียบ (อสมการ)
ถ้า แล้ว
\sqrt[3]{a} <\sqrt[3]{b}
a < b
นอกจากนี้ยังมีสมบัติของกรณฑ์ที่สามที่ควรทราบดังนี้
ต้องจำให้ได้. . .
\frac{\sqrt[3]{a}}{\sqrt[3]{b}} =\sqrt[3]{\frac{a}{b}} \ \ \ \ ;
\sqrt[3]{a} \sqrt[3]{b} =\sqrt[3]{ab}




ตัวอย่าง
และ จำนวนใดมีค่ามากกว่ากัน
\sqrt[3]{29}
\sqrt[3]{16}
เนื่องจาก 29 มีค่ามากกว่า 16
ดังนั้น มีค่ามากกว่า
\sqrt[3]{29}
\sqrt[3]{16}
ถ้า แล้ว
\sqrt[3]{a} >\sqrt[3]{b}
a > b
จากสมบัติ
จะได้ว่า
\sqrt[3]{29}
\sqrt[3]{16}
มีค่ามากกว่า

ลองทำดู
โรงงานผลิตกล่องพลาสติกแห่งหนึ่ง สำรวจพบว่ากล่องขนาดที่ขายดีที่สุดเป็นกล่องทรงลูกบาศก์ที่สามารถจุได้อย่างน้อย 1,500 ลูกบาศก์นิ้ว โรงงานต้องผลิตกล่องที่มีความยาวอย่างน้อยกี่นิ้ว (ตอบเป็นจำนวนเต็ม)

X
X
X
\text{ความจุกล่อง} =X\times X\times X
Hint!
© Aj. Krit Th.
https://www.kritth.com