ทฤษฎีบท
พีทาโกรัส
กฤษณ์ ท. AI & TECH

เนื้อหา
ในภาคเรียนนี้
A Course Syllabus

ทฤษฎีบทพีทาโกรัส
ความรู้เบื้องต้นเกี่ยวกับจำนวนจริง
ปริซึมและทรงกระบอก
การแปลงทางเรขาคณิต
สมบัติของเลขยกกำลัง
พหุนาม


สิ่งที่ต้องรู้ก่อนเรียนบทนี้
A=B^{2}=B\times B
เลขยกกำลัง:
ตัวอย่าง: จงหาค่าเลขยกกำลังของ 2
A=6^{2}=6\times 6=36
ค่ากลับของเลขยกกำลัง:
\text{เมื่อ } A=B^{2}\text{ แล้ว จะกล่าวได้ว่า } B=\sqrt{A} =A^{{}_{2}^{1}}
ตัวอย่าง: จงหาค่าสแควร์รูท (รากที่สอง) ของ 36
B=\sqrt{A} =A^{{}_{2}^{1}}=\sqrt{36} =36^{{}_{2}^{1}}
เพราะฉะนั้น
\begin{gathered}B=\text{ตัวเลขอะไรที่คูณกันเองแล้วได้ 36} =6\times 6\\ B=6\end{gathered}
#
#

แบบฝึกความเข้าใจ
3^{2}=?
จงหาค่าเลขยกกำลังต่อไปนี้
5^{2}=?
7^{2}=?
10^{2}=?
12^{2}=?
=3\times 3=9
=5\times5=25
=7\times7=49
=10\times10=100
=12\times12=144
#
\sqrt{9} =?
จงหารากที่สอง (สแควร์รูท) ต่อไปนี้
\sqrt{49} =?
\sqrt{144} =?
\sqrt{169} =?
\sqrt{64} =?
=3
=7
=12
=13
=8
#
(เพราะว่า 3 x 3 = 9)
(เพราะว่า 13 x 13 = 169)

สิ่งที่ต้องรู้ก่อนเรียนบทนี้
การย้ายข้างในสมการคณิตศาสตร์
\text{กำหนดให้ } A=B+C\text{ จะได้ว่า }
ตัวอย่าง: จงพิจารณาสมการต่อไปนี้
\text{กำหนดให้ } A=10,\ B=6,\text{ และ } C=4
#
B=A-C
C=A-B
\text{จะได้ว่า } A=B+C\text{ เท่ากับ } 10=6+4
\text{ดังนั้น } B=A-C\text{ เท่ากับ } 6=10-4
\text{ดังนั้น } C=A-B\text{ เท่ากับ } 4=10-6

แบบฝึกความเข้าใจ
กำหนดให้
100=60+40
60=100-40
40=100-60
#
\text{กำหนดให้ } A=100,\ B=60,\text{ และ } C=40
\text{จงพิสูจน์ว่า } A=B+C\text{ และ }
B=A-C
C=A-B
B=A-C
C=A-B
A=B+C
วิธีคิด

แบบฝึกความเข้าใจ
\text{กำหนดให้ } A=B+C\text{ จงหาค่าตัวแปรที่หายไป}
-
ถ้า A = 15, B = 9, C = _____
-
ถ้า A = 20, C = 7, B = _____
-
ถ้า B = 12, C = 5, A = _____
-
ถ้า A = 30, B = _____, C = 14
-
ถ้า A = _____, B = 8, C = 6
-
ถ้า A = 450, B = 275, C = _____
-
ถ้า A = 620, C = 180, B = _____
-
ถ้า B = 300, C = 125, A = _____
-
ถ้า A = 980, B = _____, C = 430
-
ถ้า A = _____, B = 150, C = 250

ทฤษฎีบทพีทาโกรัส (Pythagorus)
หลักวิธีคิด

มุมฉาก

ทฤษฎีบทพีทาโกรัส (Pythagorus)
หลักวิธีคิด

มุมฉาก
ด้านตรงข้ามมุมฉาก
ด้านประกอบมุมฉาก

ทฤษฎีบทพีทาโกรัส (Pythagorus)
หลักวิธีคิด

มุมฉาก
a
b
c
c^2=a^2+b^2

ตัวอย่าง
จากรูปสามเหลี่ยมที่กำหนดให้จงหาความยาวของด้านที่เหลือ
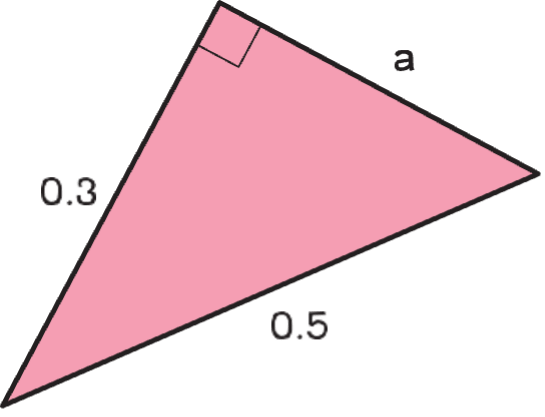

ตัวอย่าง
จากรูปสามเหลี่ยมที่กำหนดให้จงหาความยาวของด้านที่เหลือ
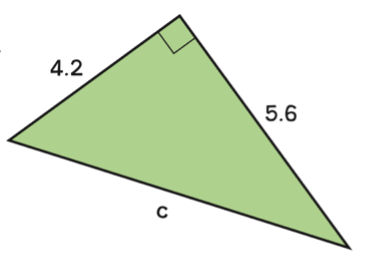

ตัวอย่าง
จากรูปสามเหลี่ยมที่กำหนดให้จงหาความยาวของด้านที่เหลือ
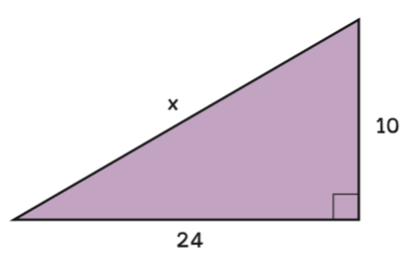

ตัวอย่าง
จากรูปสามเหลี่ยมที่กำหนดให้จงหาความยาวของด้านที่เหลือ
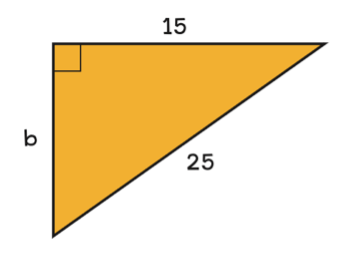

ตัวอย่าง
1. ABCD เป็นรูปสี่เหลี่ยมผืนผ้ามีด้านกว้าง 24 เมตร ยาว 32 เมตร เส้นทแยงมุมยาวเท่าใด
2. ABCD เป็นรูปสี่เหลี่ยมคางหมูมี AB ตั้งฉากกับ AD และ CD ยาว 6 หน่วย
AB ยาว 12 หน่วย BC ยาว 6 2 หน่วย จงหาว่ารูปสี่เหลี่ยม ABCD มีส่วนสูงเท่าไร

ตัวอย่าง
3. ให้สามเลี่ยม ABC เป็นรูปสามเหลี่ยมด้านเท่าที่มีด้านทั้งสามยาวด้านละ 4 เซนติเมตร จงหาความสูงของรูปสามเหลี่ยม
4. น้อยหน่าเดินทางไปทางทิศตะวันออกได้ 24 ไมล์ แล้วเลี้ยวไปทางทิศเหนืออีก 32 ไมล์ จงหาว่าน้อยหน่าอยู่ห่างจากจุดเริ่มต้นกี่ไมล์

ตัวอย่าง
5. ต้นไม้ต้นหนึ่งใช้เชือกผูกที่จุดจุดหนึ่งซึ่งอยู่ห่างจากยอดต้นไม้ 2 ฟุต แล้วดึงมาผูกที่หลักซึ่งอยู่ห่างจากโคนต้นไม้ 15 ฟุต ถ้าเชือกยาว 25 ฟุต แล้วต้นไม้จะสูงเท่าใด

ลองคิดดู
ในการขึ้น–ลงจากเครื่องบิน ถ้าเครื่องบินไม่ได้เข้ามาเทียบท่าที่สะพานเทียบเครื่องบิน ก็จะมีบันไดเทียบเครื่องบินสำหรับให้ผู้โดยสารขึ้น–ลงจากเครื่องบิน
ซึ่งบันไดเทียบเครื่องบินจะมีทางเดินก่อนลงบันได ถ้าบันไดเทียบเครื่องบินอันหนึ่งมีทางเดินก่อนลงบันไดขั้นแรกยาว 1.20 เมตร ความยาวของบันไดเป็น 6 เมตร และบันไดขั้นสุดท้ายอยู่สูงจากพื้น 0.25 เมตร
เมื่อเทียบบันไดกับเครื่องบินแล้ว เชิงบันไดจะอยู่ห่างจากแนวประตูเครื่องบิน 6 เมตร ดังรูป อยากทราบว่าทางเดินก่อนลงบันไดนี้จะอยู่สูงจากพื้นกี่เมตร

ลองคิดดู
บ้านของมีนา โรงเรียน และที่ทำงานของคุณพ่อ อยู่ในตำแหน่งที่เป็นจุดยอดของรูปสามเหลี่ยมมุมฉาก
โดยที่ทำงานของคุณพ่ออยู่ห่างจากบ้านของมีนา 1.5 กิโลเมตร และอยู่ห่างจากโรงเรียน 2 กิโลเมตร
ตอนเช้ามีนาขี่จักรยานจากบ้านตรงไปที่โรงเรียนโดยไม่ผ่านที่ทำงาน แต่ทุก ๆ วันหลังเลิกเรียน มีนาต้องไปหาคุณพ่อก่อนที่จะกลับบ้าน
อยากทราบว่าในแต่ละวันมีนาจะขี่จักรยานเป็นระยะทางอย่างน้อยกี่กิโลเมต
© Aj. Krit Th.
https://www.kritth.com