คณิตศาสตร์คอมพิวเตอร์
ตรรกศาสตร์ (Logics)
ตัวอย่าง พีชคณิตเชิงเส้น
จากสมการเชิงเส้น
2X+3Y=8
X-2Y=-3
จงหาค่าตัวแปร X, และ Y
จงหาค่าตัวแปร X, และ Y
X = 1
Y = -2
พีชคณิตบูลีน
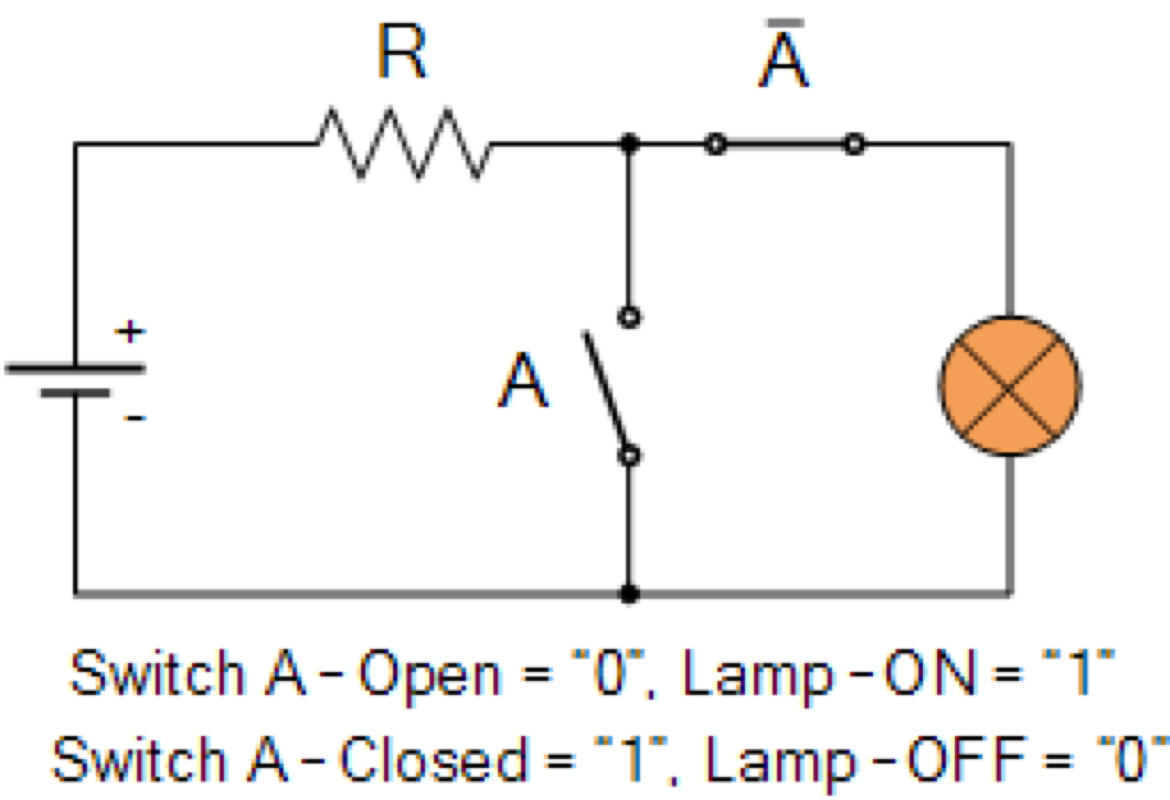
เครื่องคอมพิวเตอร์ = ระบบดิจิทอล

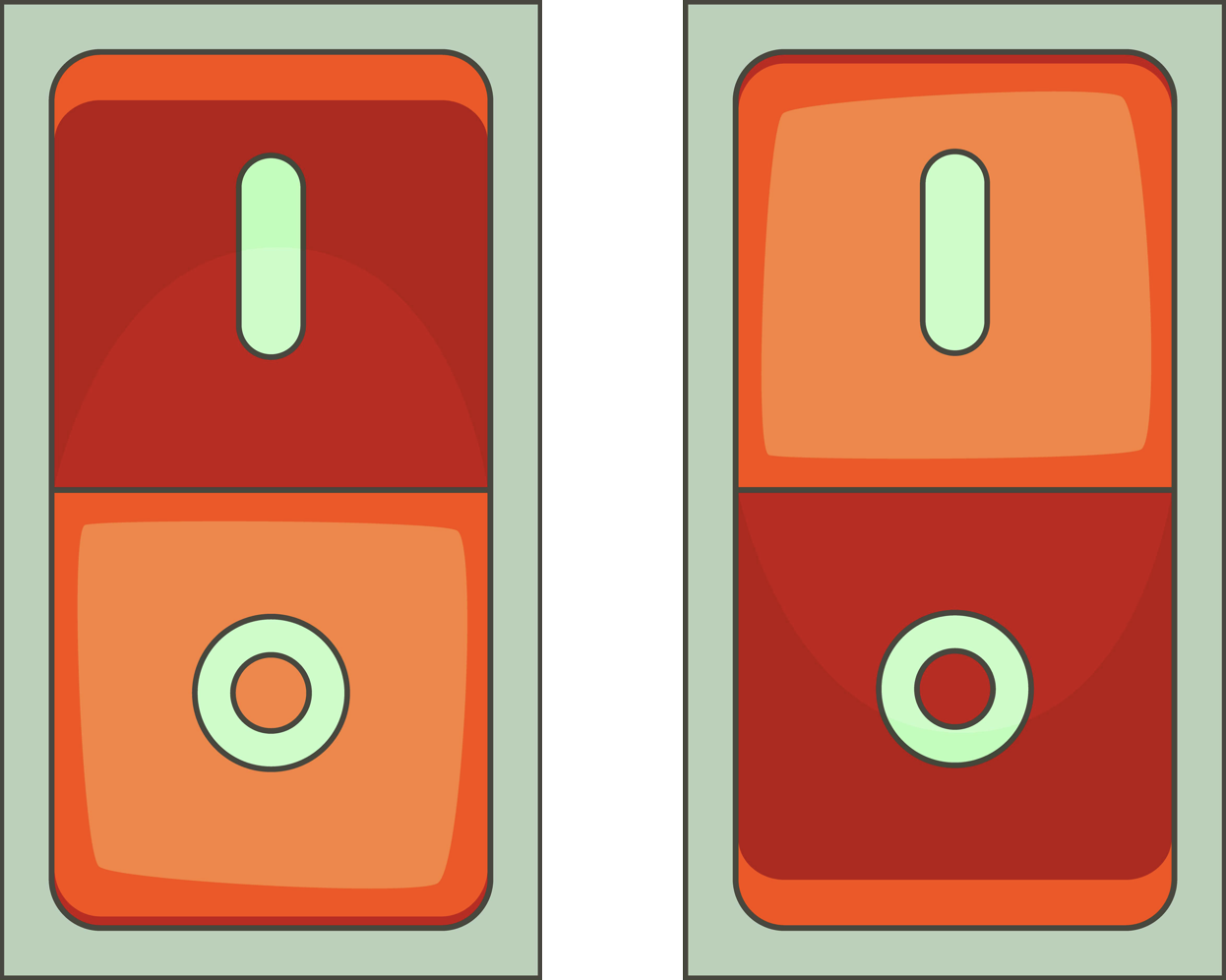


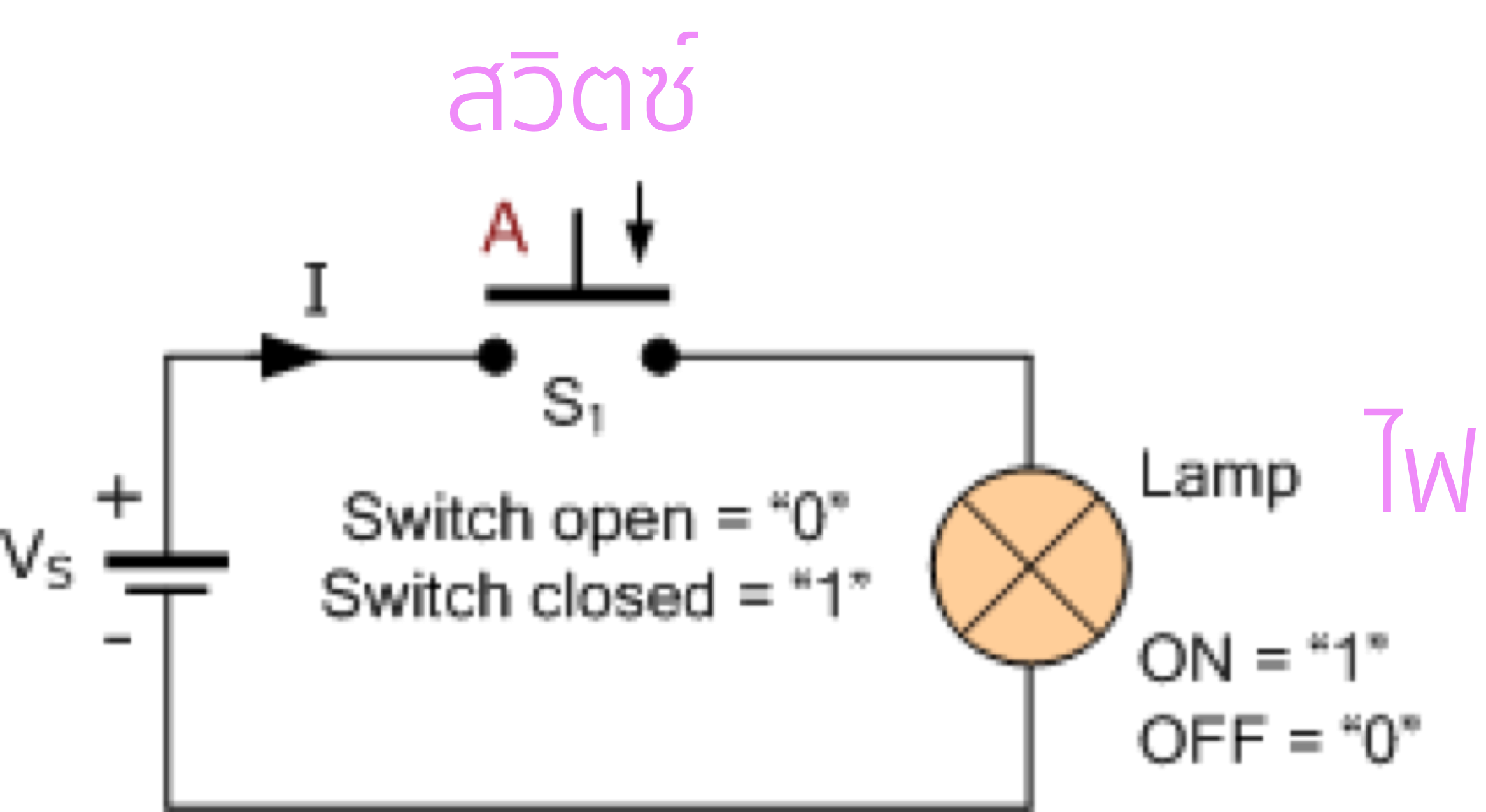
| A สวิตซ์ | L ไฟ |
|---|---|
| 0 | 0 |
| 1 | 1 |
ไฟดับ
ไฟติด
ตัวอย่าง วงจรหน่วยความจำ (D Flip-Flop)
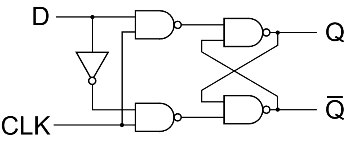
วงจรไฟฟ้า (ดิจิทอล) อย่างง่ายที่เป็นต้นแบบของอุปกรณ์หน่วยความจำ (RAM) ในเครื่องคอมพิวเตอร์ สามารถจำตำแหน่งสถานะของข้อมูลได้


โลจิกพื้นฐาน (Gate - เกต)
-
AND (และ)
-
OR (หรือ)
-
NOT (นิเสธ)
-
NAND / NOR
-
XOR / XNOR
พีชคณิตบูลีน
-
กฎ - ทฤษฎี
-
การลดรูปวงจรอย่างง่าย

AND (และ) Gate

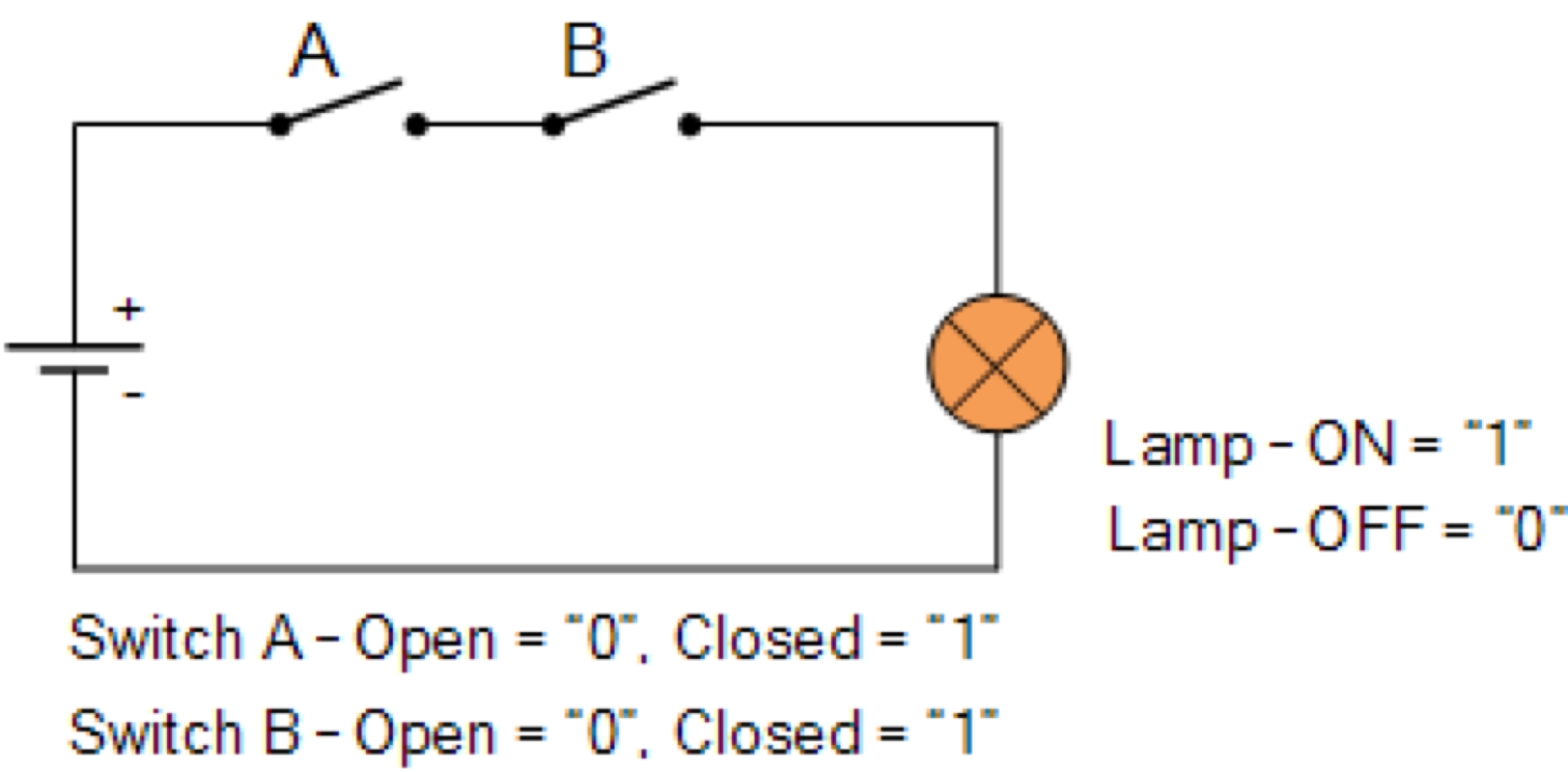
| A | B | Q (A . B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
สัญญลักษณ์ที่ใช้
& หรือ . หรือ
\wedge
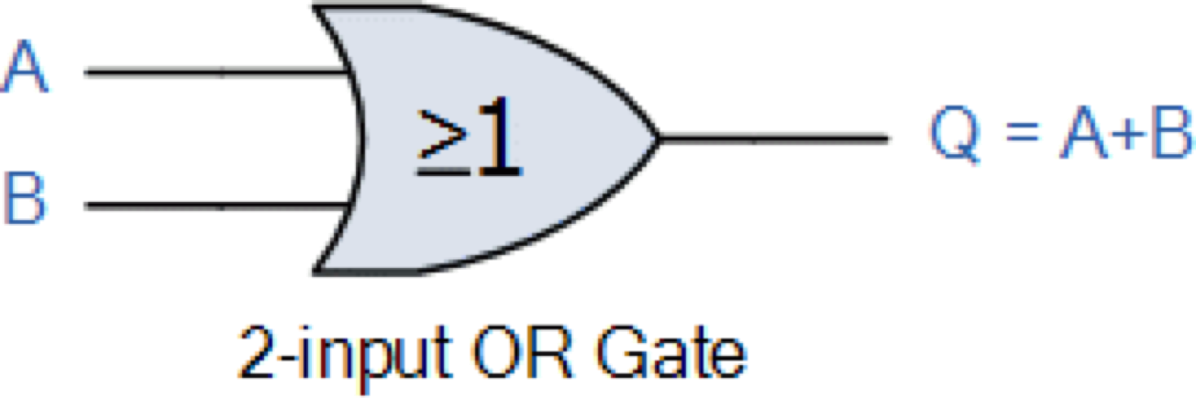
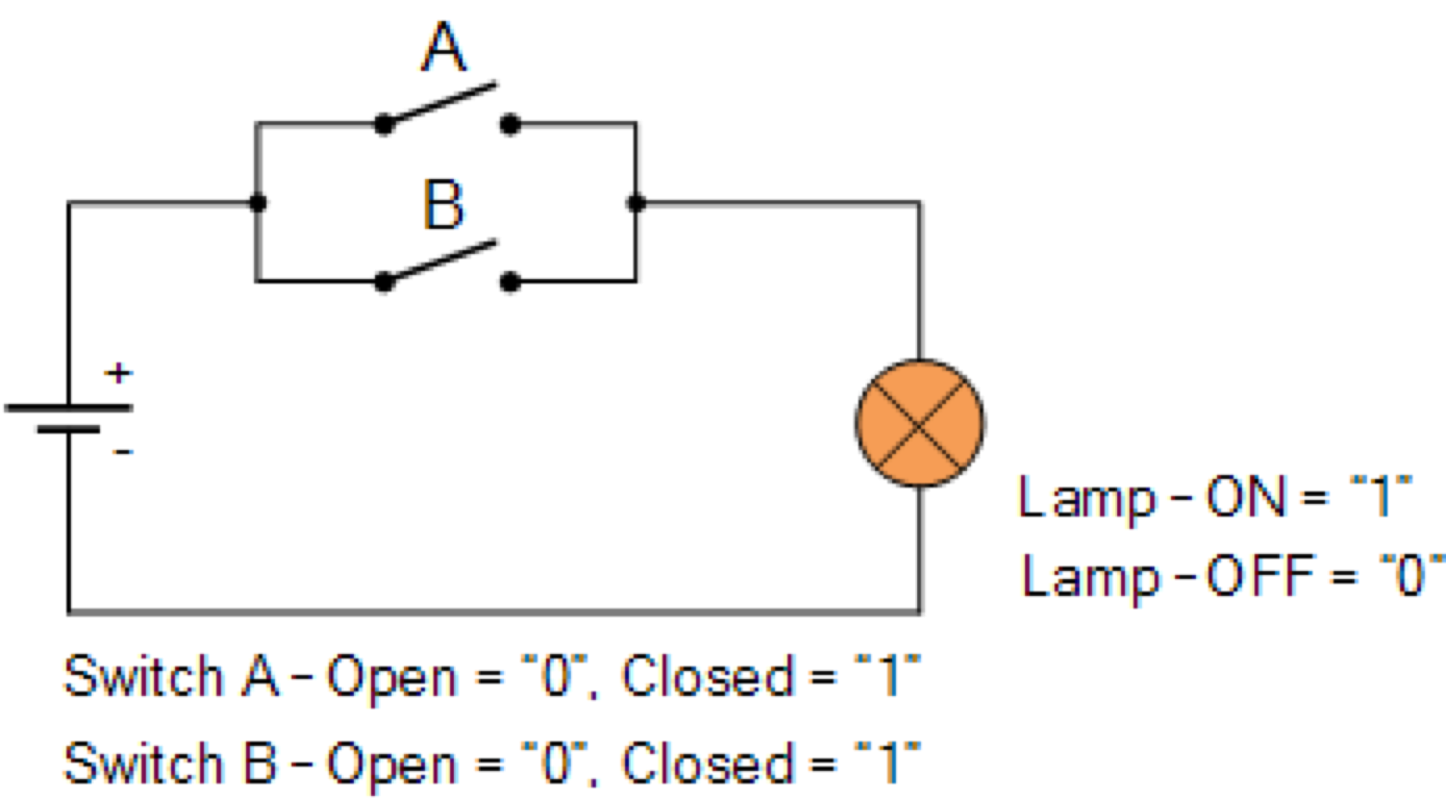
OR (หรือ) Gate
| A | B | Q (A + B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
สัญญลักษณ์ที่ใช้
+ หรือ
\vee
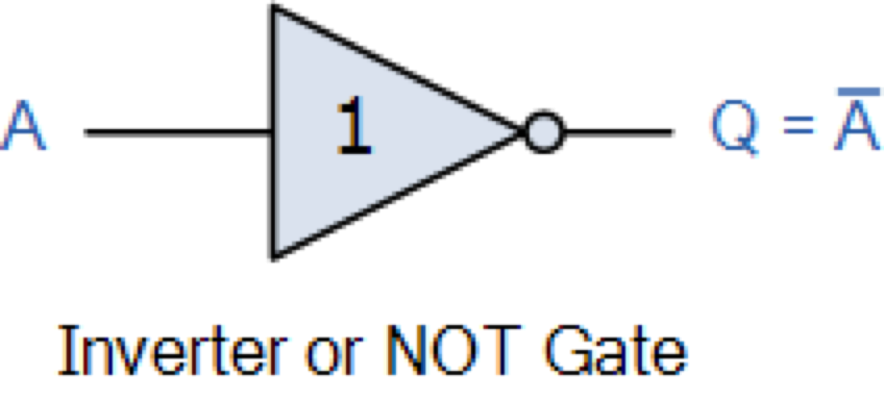
NOT (นิเสธ) Gate
| A | |
|---|---|
| 0 | 1 |
| 1 | 0 |
สัญญลักษณ์ที่ใช้
~ หรือ
\overline{A}
_
NAND Gate
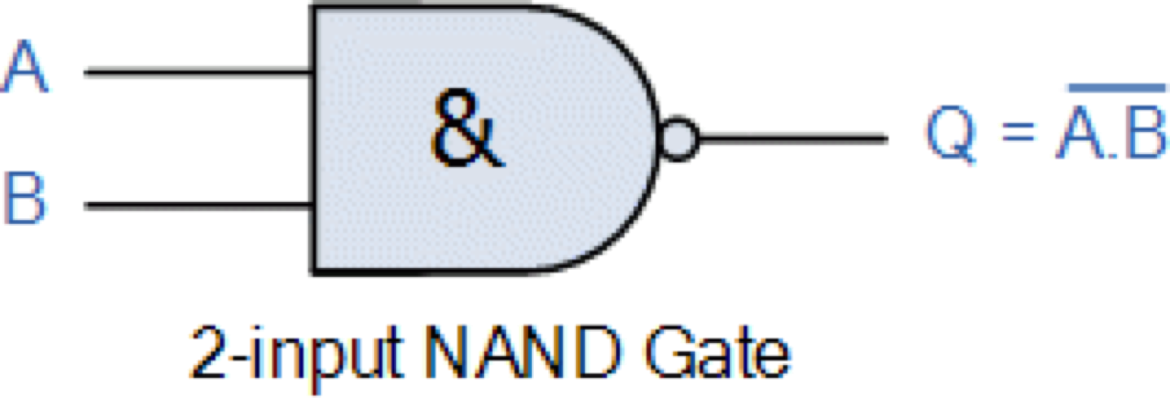
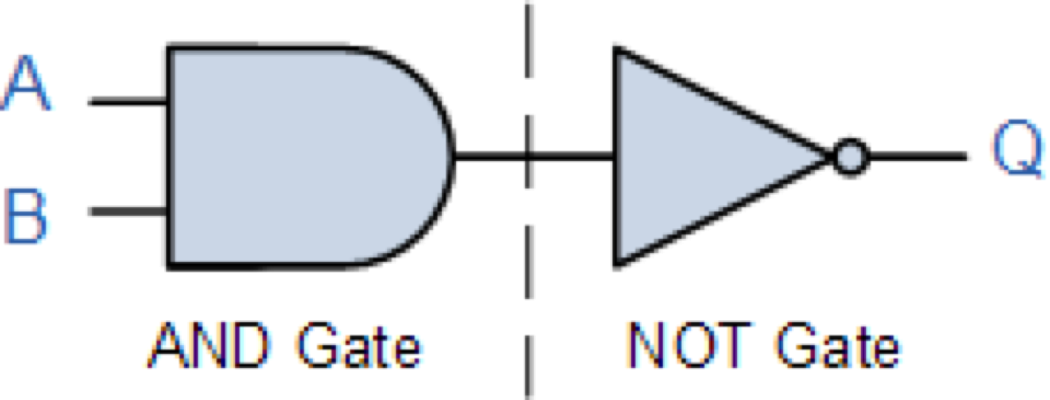
หรือ
| A | B | |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
\overline{A.B}
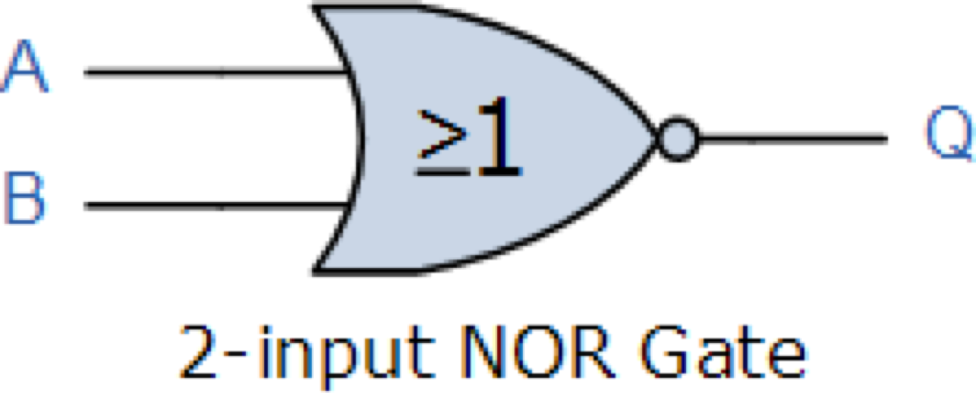
NOR Gate
หรือ
| A | B | |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
\overline{A+B}
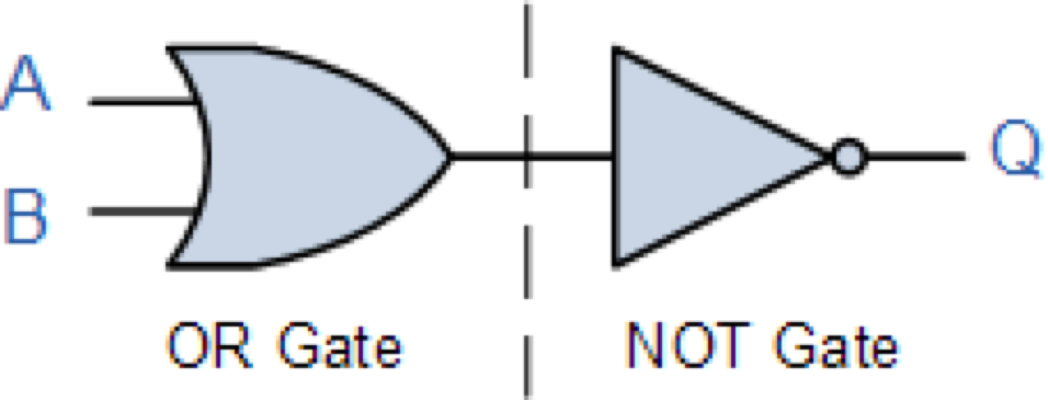
XOR Gate
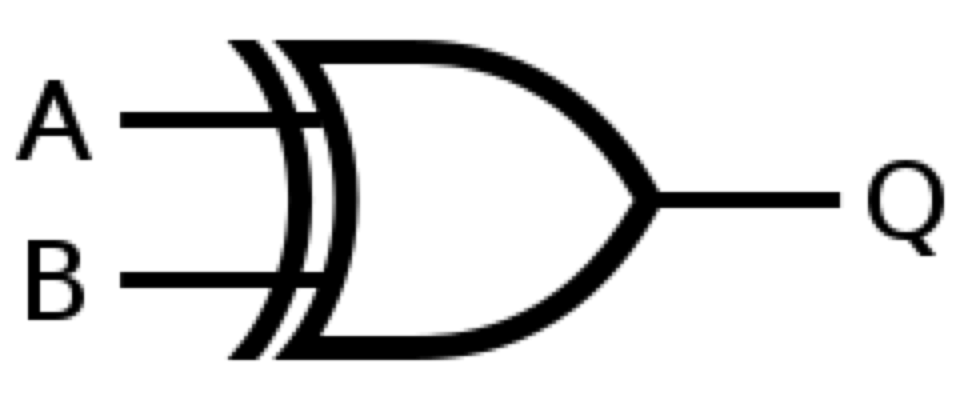
สัญญลักษณ์ที่ใช้
\oplus
| A | B | |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
\left( A.\overline{B} \right) +\left( \overline{A} .B\right)
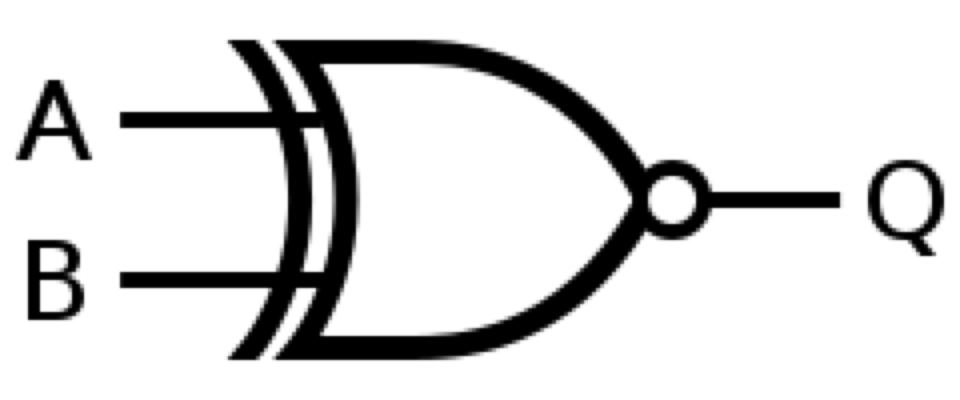
XNOR Gate
| A | B | |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
\overline{\left( A.\overline{B} \right) +\left( \overline{A} .B\right)}
Truth Tables (ตารางความจริง)
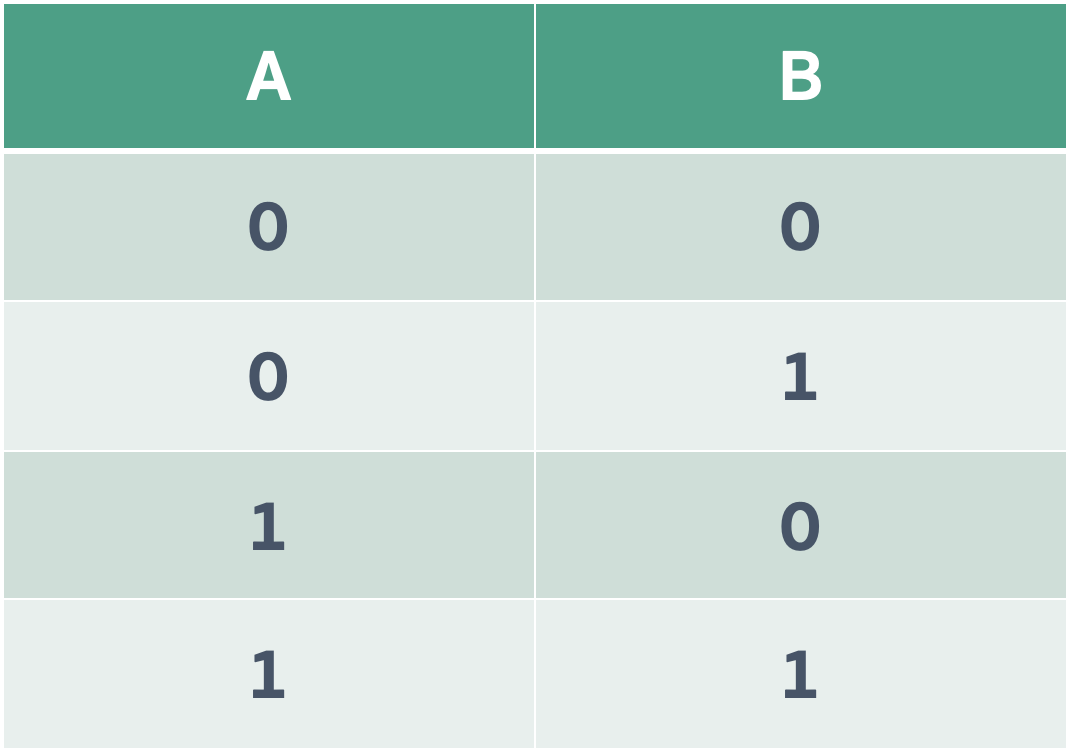
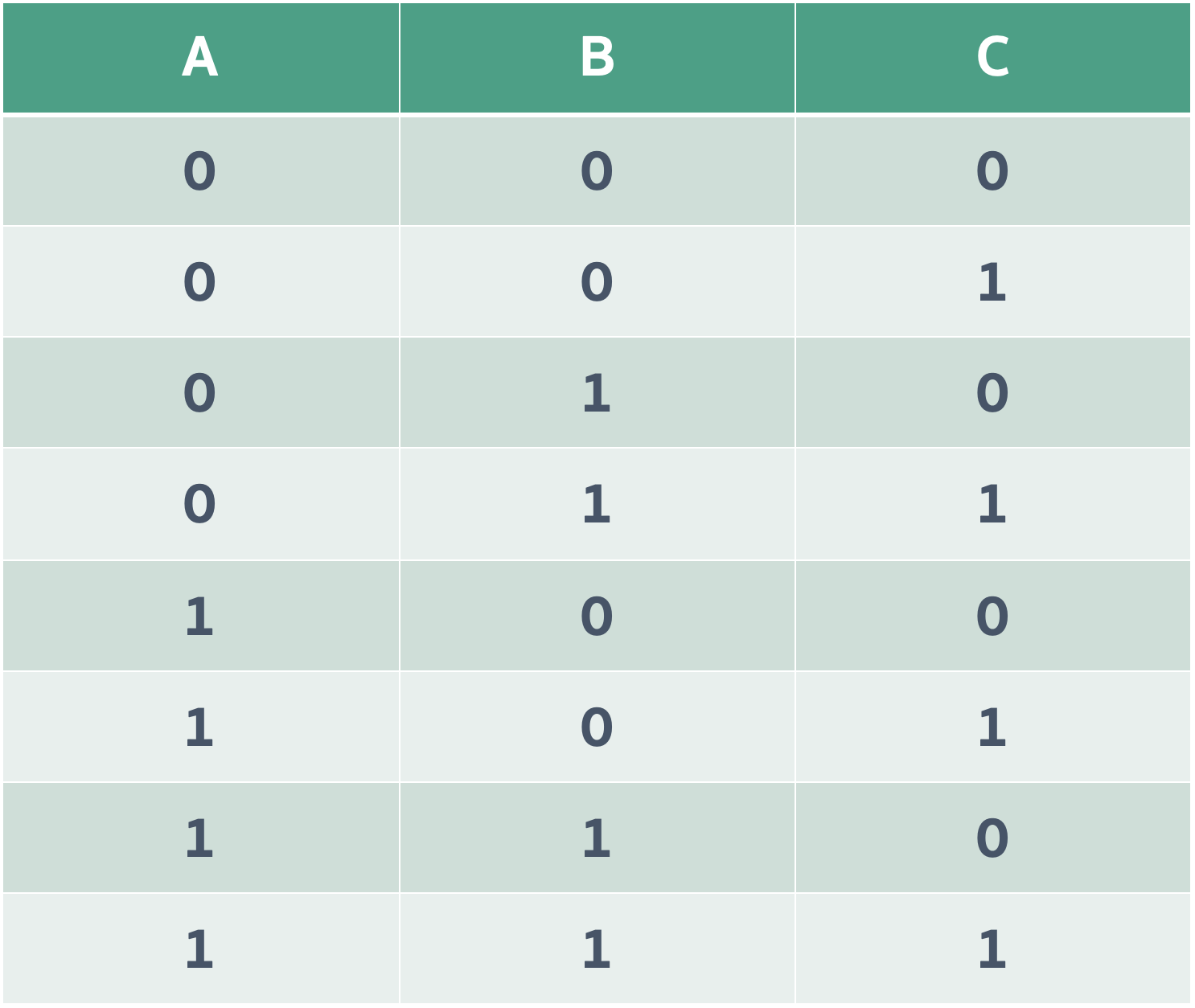
2 ตัวแปร
3 ตัวแปร
ตัวอย่าง
กำหนดให้
f_{1}\left( x{}_{1},x_{2}\right) =\left( \overline{x_{1}+x_{2}} \right)
f_{2}\left( x{}_{1},x_{2}\right) =\left( \overline{x_{1}} .\overline{x_{2}} \right)
และ
จงพิสูจน์ว่า
f_{1}\left( x{}_{1},x_{2}\right) =f_{2}\left( x{}_{1} ,x_{2}\right)
สรุป Gate
| คำอธิบาย | # 1 | # 2 | # 3 |
|---|---|---|---|
| AND (และ) | |||
| OR (หรือ) | |||
| NOT (นิเสธ) | |||
| NAND | |||
| NOR | |||
| XOR | |||
| XNOR |
.
+
-
\overline{a+b}
\overline{a.b}
\left( a.\overline{b} \right) +\left( \overline{a} .b\right)
\overline{\left( a.\overline{b} \right) +\left( \overline{a} .b\right)}
\bigwedge
\bigvee
\prime
\text{} a\oplus b
\overline{\text{} a\oplus b}







ตัวอย่าง
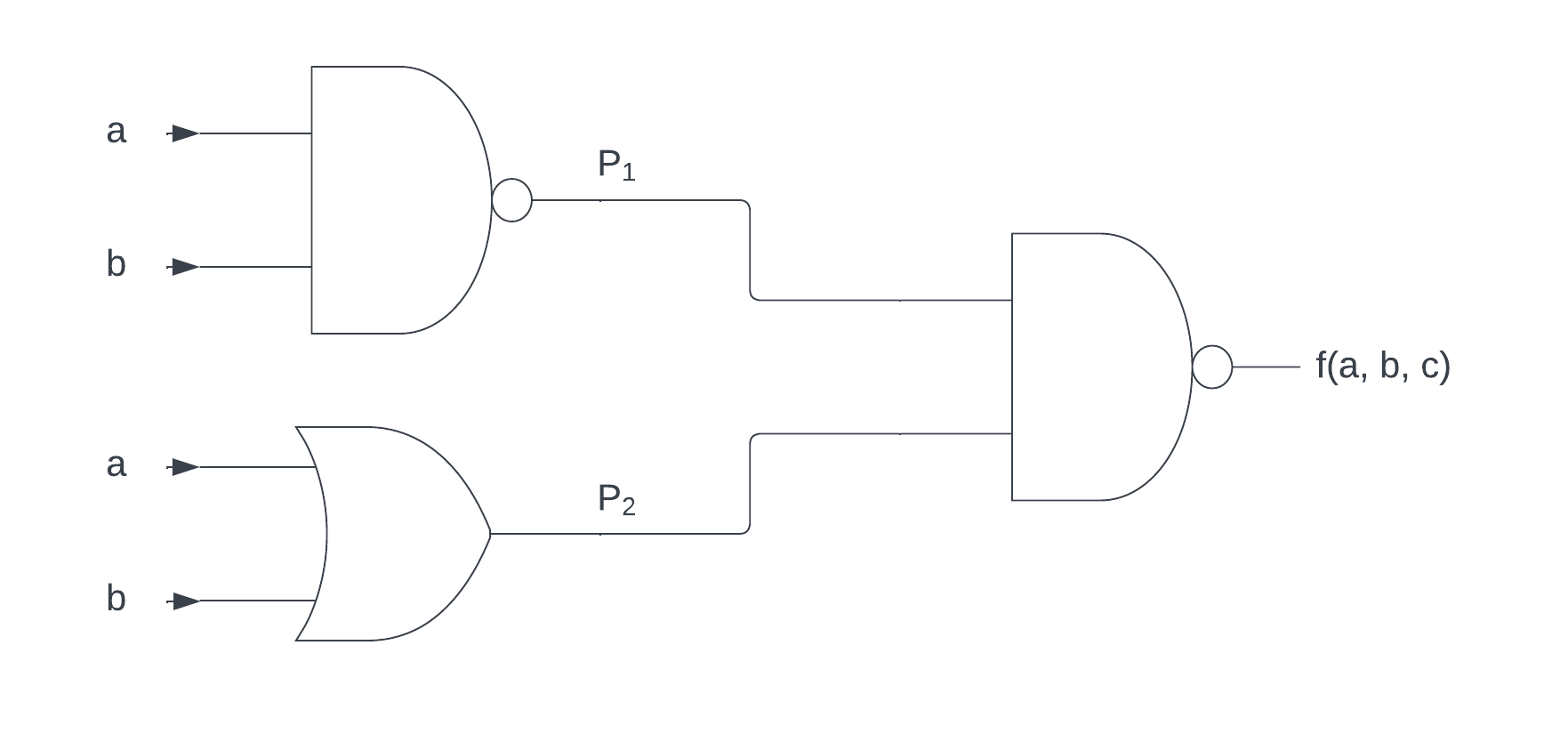
จงเขียนสวิตชิ่งฟังก์ชั่นของวงจรโลจิกต่อไปนี้
ตัวอย่าง
จงเขียนวงจรลอจิกของสมการ
f\left( a,b,c\right) =\left( \left( a.b\right) +\left( a.c\right) \right) +\overline{c}
กฎพื้นฐานของพีชคณิตบูลีน
กำหนดให้ w, x, y, และ z เป็นตัวแปรเดี่ยว
x.0=0
x.1=x
x.x=x
x.\overline{x} =0
x+0=x
x+1=1
x+x=x
x+\overline{x} =1
x+y=y+x
x.y=y.x
กฎพื้นฐานของพีชคณิตบูลีน
กำหนดให้ w, x, y, และ z เป็นตัวแปรเดี่ยว
x+\left( y+z\right) =\left( x+y\right) +z=x+y+z
x\left( yz\right) =\left( xy\right) z=xyz
x(y+z)=xy+xz
\left( w+x\right) (y+z)=wy+xy+wz+xz
กฎพื้นฐานของพีชคณิตบูลีน
กำหนดให้ w, x, y, และ z เป็นตัวแปรเดี่ยว
x+\overline{x} y=x+y
x+yx=x
จงพิสูจน์ ทฤษฎี ด้านบน
ตัวอย่าง
ถ้า p เป็นเท็จ q เป็นจริง r เป็นเท็จ และ s เป็นจริง จงหาค่าความจริงของประพจน์
\left( p.q\right) +\left( r.\overline{s} \right)
สัจนิรันด์ (Tautology)
สันจนิรันด์หมายถึง ประพจน์ที่มีค่าความจริงเป็นจริงทุกกรณี ตัวอย่าง
\overline{p\oplus \overline{\overline{p} } }
\overline{\left( p.q\right) } \oplus \left[ \overline{p} +\overline{q} \right]
ตัวอย่าง
จงตรวจสอบว่าประพจน์แต่ละคู่ต่อไปนี้สมมูล*กันหรือไม่
\left[ p+\left( q.r\right) \right] \text{กับ} \left( p+q\right) .\left( p+r\right)
* สมมูล หมายถึง มีผลลัพธ์เหมือนกันทุกประการ
กฎ ทฤษฎี เดอร์มอร์แกน (De Morgan's Law)
\left( \overline{x+y} \right) =\overline{x} .\overline{y}
\left( \overline{x.y} \right) =\overline{x} +\overline{y}
ตัวอย่าง
Y=\left( \overline{A\overline{B} +C} \right)
จงลดรูปสมการต่อไปนี้
© Aj. Krit Th.
https://www.kritth.com