คณิตศาสตร์คอมพิวเตอร์

ระบบจำนวน

E-Learning

  1. เข้าไปที่ classroom.google.com

  2. คลิ้กเครื่องหมาย + และเลือก Join class

  3. กรอกรหัส ksjzinq ในกล่องข้อความ และ คลิ้ก Join

  4. เปลี่ยน ชื่อ นามสกุล ให้เป็นชื่อและนามสกุลจริง

ksjzinq

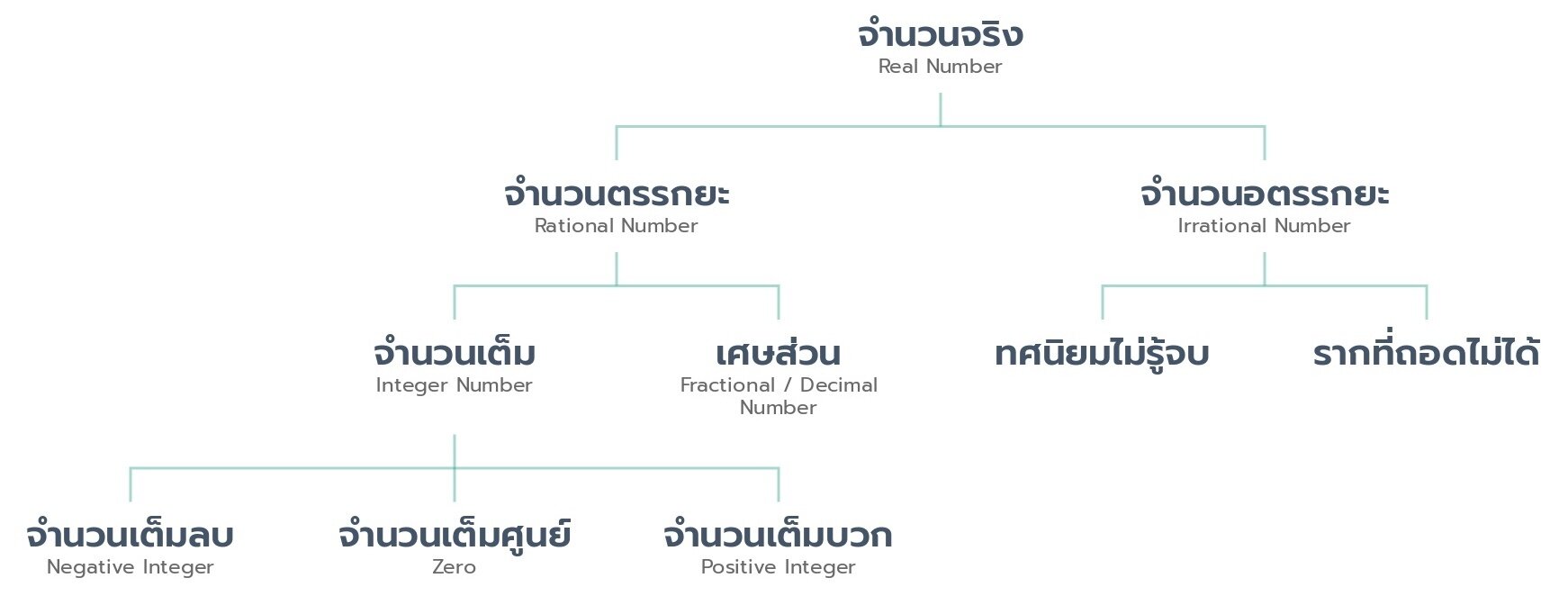
ระบบจำนวน

คอมพิวเตอร์กับเลขฐาน

ระบบเลขฐาน

เมตริกซ์

พีชคณิตบูลีน

ตรรกศาสตร์

วิวัฒนาการของระบบจำนวน

ความคิดทางคณิตศาสตร์ยุคบาบิโลเนีย

  1. ชีวิตความเป็นอยู่ของมนุษย์อยู่กับธรรมชาติ

  2. การเฝ้าสังเกตเห็นการเปลี่ยนแปลง

  3. การกำหนดทิศเหนือ ใต้

  4. รับรู้เรื่องเวลา-เวียนรอบครบอีกหนึ่งครั้งโดยแบ่งเป็นวัน

  5. การแบ่งเวลาเป็นชั่วโมงและนาที

  6. พบเรื่องราวฤดูกาลและปี

  7. เลขฐาน 60 คือพื้นฐาน "นาที" ในปัจจุบัน

วิวัฒนาการของระบบจำนวน

ความคิดทางคณิตศาสตร์ยุคสมัยอิยิปต์และโรมัน

  • ตัวเลขแบบไฮราติก สัญลักษณ์ทั้งหมด 36 ตัว

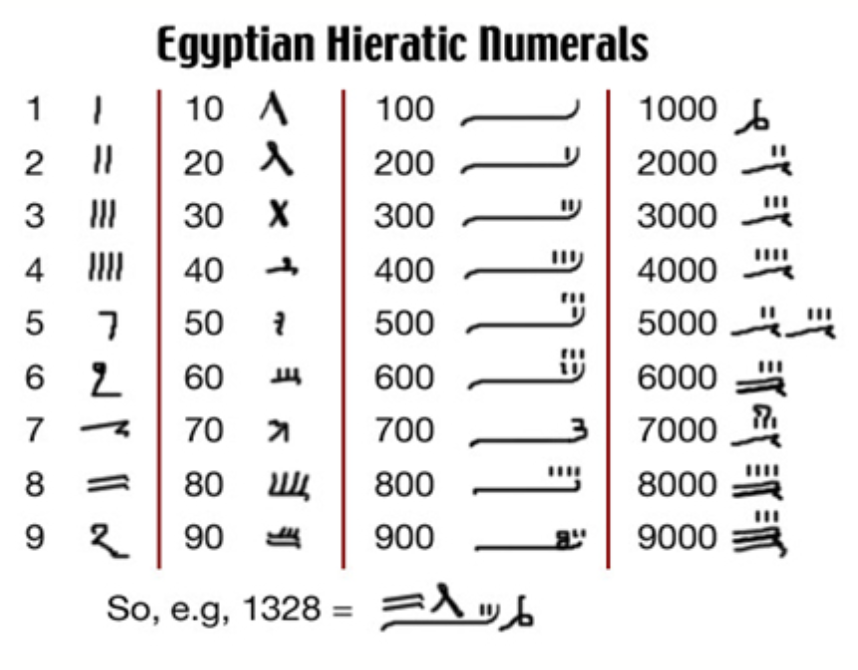
ความคิดทางคณิตศาสตร์ยุคสมัยอิยิปต์และโรมัน

สมัยกรีก

  1. เธลีส (Thales 640-546 B.C.)

  2. ปีทาโกรัส (Pythagoras 580-496 B.C.)

  3. อาร์คีมีดีส (Archimedes 287-212 B.C.)

ความคิดทางคณิตศาสตร์ยุคสมัยอิยิปต์และโรมัน

สมัยกลาง

  1. ประมาณ ค.ศ. 529-1436 วิธีเขียนตัวเลขใหม่จากอินเดีย ตัวเลข 1 2 3 4 5 6 7 8 9 0  ที่ใช้กันทุกวันนี้

  2. ประมาณ ค.ศ. 1437-1600 หลังสงครามครูเสด ชาวยุโรปแล่นเรือไปค้าขายทั่วโลก มีการใช้สัญญลักษณ์ + และ -

  3. ตำราคณิตศาสตร์แพร่หลายในยุคนี้ รวมถึงการตั้งหารยาว

  4. นำคณิตศาสตร์ไปคำนวณดาราศาสตร์ -> โลกหมุน

  5. เนเปอร์ จ. เนเปียร์ / แบลส ปาสกาล / เซอร์ไอแซก นิวตัน

Neper John Napier

Blaise Pascal

Sir Isaac Newton

ความคิดทางคณิตศาสตร์ยุคสมัยอิยิปต์และโรมัน

สมัยปัจจุบัน

  1. คาร์ล ฟรีดริค เกาส์ (Carl Friedrich Gauss ค.ศ. 1777-1855) พีชคณิต ทฤษฎีจำนวน การวิเคราะห์เชิงตัวเลข

  2. นีลส์ เฮนริก อาเบล (Niels Henrik Abel ค.ศ. 1802-1829)

  3. อัลเบิร์ต ไอน์สไตน์ (Albert Einstein ค.ศ. 1879-1955) นักฟิสิกส์ชาวเยอรมัน ใช้คณิตศาสตร์สร้างทฤษฎีสัมพันธภาพ

  4. คณิตศาสตร์แขนงใหม่ในสมัยปัจจุบัน ทฤษฎีเซต กำเนิดเมื่อ ค.ศ. 1892 โทโพโลยี ค.ศ. 1895 ทฤษฎีการเสี่ยง ค.ศ. 1931 และกำหนดการเชิงเส้น กำเนิดเมื่อ ค.ศ. 1947

จำนวนและตัวเลข

  1. จำนวน (Number) หมายถึง ตัวบ่งชี้ปริมาณ ซึ่งเป็นผลมาจากตัวเลข (Numeral) ประกอบกัน

  2. ตัวเลข (Numeral) หมายถึง

    • สื่อหรือสัญลักษณ์แทนการนับจำนวน

    • ถือกำเนิดมาเพื่อหลายพันปีก่อน

    • เช่น ตัวเลขฮินดูอารบิก ซึ่งประกอบไปด้วยตัวเลข 10 ตัว คือ 0, 1, 2, 3, 4, 5, 6, 7, 8 และ 9

    • ซึ่งเมื่อค่าของจำนวนมีค่ามากกว่า 9 ขึ้นไปจะเกิดการประกอบกันขึ้นมาของตัวเลขทั้ง 10 (การเพิ่มหลัก)

โครงสร้างและระบบจำนวน

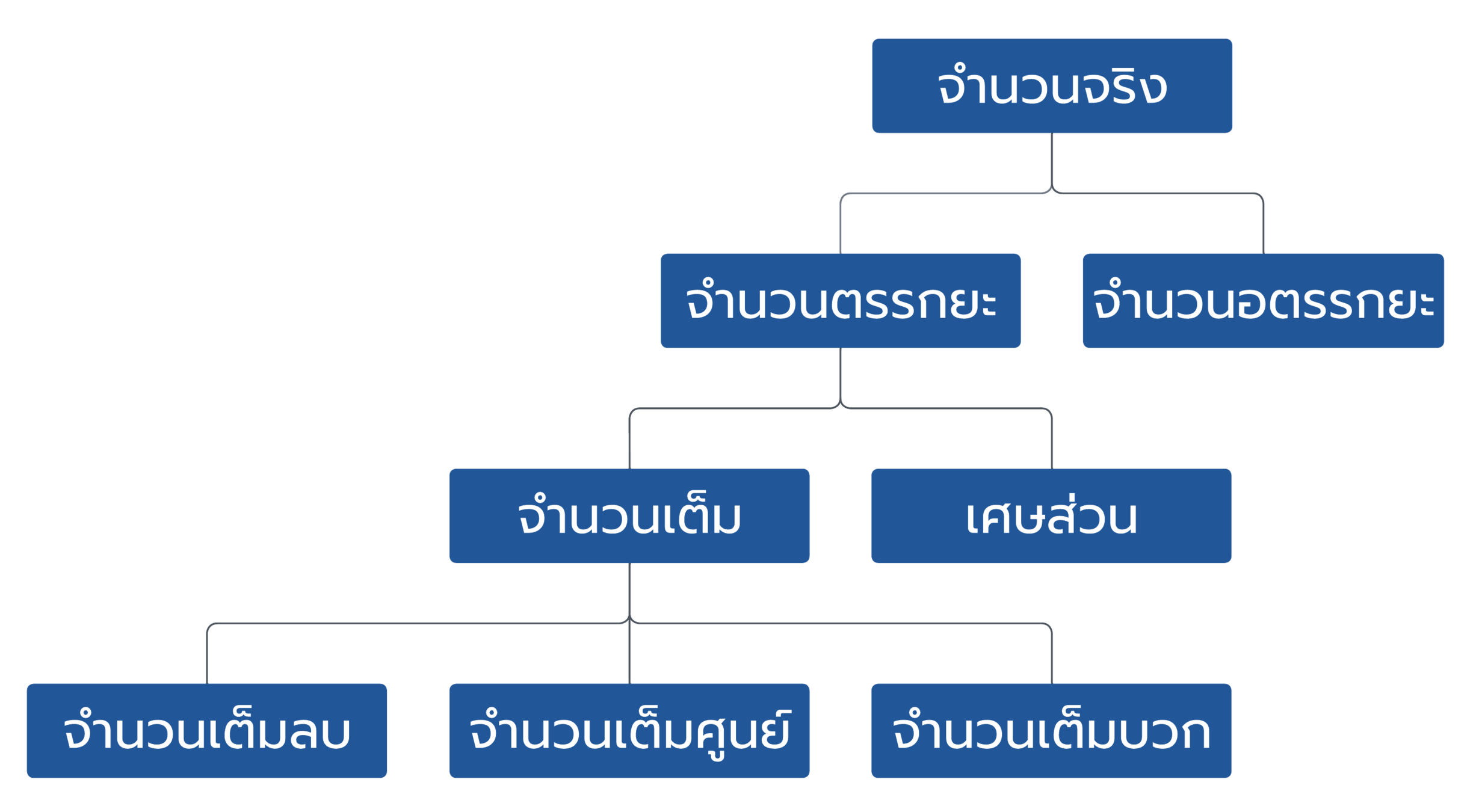
จำนวนเต็ม

โครงสร้างและระบบจำนวน

เศษส่วน

โครงสร้างและระบบจำนวน

\frac{A}{B}

  • A และ B เป็นจำนวนเต็ม

  • B จะต้องไม่เท่ากับศูนย์

\frac{3}{2}

เช่น

เศษส่วน

ตัวอย่าง

\frac{3}{3} =1

เศษส่วน

ตัวอย่าง

\frac{3}{2} =1.5

ได้คนละ 1 ลูกครึ่ง (ครึ่ง = .5)

เศษส่วนสามารถเขียนแปลงให้อยู่ในรูปของ ทศนิยม ได้

เช่นเดียวกัน ทศนิยม สามารถเขียนแปลงให้อยู่ในรูปของเศษส่วนได้

 

ทักษะ: การหาร

เลขมีหลักและไม่มีหลัก

โครงสร้างและระบบจำนวน

  1. เลขมีหลัก (Position Notation) ยกตัวอย่างเช่น จงวิเคราะห์ตัวเลข 25,921  1,312,937 และ 631

  2. เลขไม่มีหลัก ยกตัวอย่าง เช่น เลขโรมัน สัญญลักษณ์แทนตัวเลข-จำนวน ในภาษาต่าง ๆ

เลขมีหลักและไม่มีหลัก

ตัวอย่าง

จงตอบคำถามต่อไปนี้

  1. 67824 เลข 7 มีค่าเท่าใด

  2. 1293 เลข 9 มีค่าเท่าใด

  3. จงแจกแจงค่าของเลขทุกหลักสำหรับ 67824

  4. จงแจกแจงค่าของเลขทุกหลักสำหรับ 1293

เลขมีหลักและไม่มีหลัก

ตัวอย่าง

จงยกตัวอย่างตัวเลขที่ไม่มีหลัก

เลขฐานวิทยาศาสตร์

โครงสร้างและระบบจำนวน

เลขฐานวิทยาศาสตร์ (Scientific Notation) นำมาใช้เพื่อลดรูปของตัวเลขปกติ เพื่อแสดงค่าของจำนวนมากและสื่อให้เข้าใจตรงกัน เช่น 1,234,000,000,000

10^{0}=1
10^{1}=10
10^{2}=100
10^{3}=1000
10^{4}=10000
10^{-1}=0.1
10^{-2}=0.01
10^{-3}=0.001
10^{-4}=0.0001
10^{-5}=0.00001
=1.234\times 10^{12}

เลขฐานวิทยาศาสตร์

ตัวอย่าง

จงแปลงค่าเลขต่อไปนี้ให้อยู่ในรูปเลขยกกำลัง (วิทยาศาสตร์)

  1. 15900

  2. 817

  3. 0.681

  4. 0.002394

จงแปลงเลขยกกำลัง (วิทยาศาสตร์) ให้อยู่ในรูปแบบปกติ

  1.  

  2.  

9\times 10^{1}
3.87\times 10^{-7}

คุณสมบัติเกี่ยวกับการบวก

คุณสมบัติพื้นฐานของระบบจำนวนจริง

  1. คุณสมบัติปิดของการบวก ถ้า a และ b เป็นจำนวนจริงแล้ว ผลลัพธ์ a + b ย่อมเป็นจำนวนจริง

  2. คุณสมับัติการสลับที่ a + b = b + a

  3. คุณสมับติการจัดหมู่ (a + b) + c = a + (b + c)

  4. เอกลักษณ์ของการบวก คือ 0 ได้แก่ a + 0 = a

  5. อินเวอร์สการบวก a + (-a) = (-a) + a = 0

คุณสมบัติเกี่ยวกับการคูณ

คุณสมบัติพื้นฐานของระบบจำนวนจริง

  1. คุณสมบัติปิดของการคูณ ถ้า a และ b เป็นจำนวนจริงแล้ว ผลลัพธ์ a x b ย่อมเป็นจำนวนจริง

  2. คุณสมบัติการสลับที่ a x b = b x a

  3. คุณสมบัติการจัดกลุ่ม (a x b) x c = a x (b x c)

  4. เอกลักษณ์ของการคูณคือ 1 ได้แก่ a x 1 = 1

  5. อินเวอร์สของการคูณคือ      ได้แก่

a^{-1}
a\times a^{-1}=1

เอกลักษณ์/อินเวอร์ส การบวก คือ 0

เอกลักษณ์/อินเวอร์ส การคูณ คือ 1

คุณสมับติเกี่ยวกับการลบและการหาร

คุณสมบัติพื้นฐานของระบบจำนวนจริง

  1. การลบ คือ การบวกด้วยค่าอินเวอร์สของตัวลบ
    เช่น a - b = a + (-b)

  2. การหาร คือ การคูณด้วยอินเวอร์สของการหาร
    เช่น

\frac{a}{b} =ab^{-1}
b\neq 0

เมื่อ

คุณสมับติเกี่ยวกับเลขยกกำลัง

คุณสมบัติพื้นฐานของระบบจำนวนจริง

  1. การยกกำลังของเลขจำนวนจริงใด ๆ มีค่าเท่ากับการคูณของเลขจำนวนจริงนั้น ๆ ตามจำนวน (ครั้ง) ของเลขยกกำลัง เช่น

  2.  

  3.  

  4.  

  5.  

  6.  

2^{4}=2\times 2\times 2\times 2
\left( a^{m}\right)^{n} =a^{m\times n}
\left( a\times b\right)^{n} =a^{n}\times b^{n}
\left( \frac{a}{b} \right)^{n} =\frac{a^{n}}{b^{n}}
a^{0}=1
a^{m}\times a^{n}=a^{mn}
a^{m}. a^{n}=a^{mn}

หรือ

คุณสมับติเกี่ยวกับเลขยกกำลัง

คุณสมบัติพื้นฐานของระบบจำนวนจริง

  1. d

  2.  

  3.  

a^{\frac{1}{n} }=\sqrt[n]{a}
a^{-n}=\frac{1}{a^{n}}
\frac{a^{m}}{a^{n}} =a^{m-n}

คุณสมบัติการเท่ากัน

ความสัมพันธ์ในระบบจำนวนจริง

  1. a = a

  2. สมมาตร ถ้า a = b แล้ว b = a

  3. ถ่ายทอด ถ้า a = b และ b = c แล้ว a = c

  4. การเพิ่มแบบเท่ากัน ถ้า a = b แล้ว จะได้ a + c = b + c
    หรือ a = b แล้ว จะได้ว่า a x c = b x c

  5. การลดทอนแบบเท่ากัน ถ้า a + c = b + c จะได้ a = b
    หรือ a x c = b x c จะได้ a = b

คุณสมบัติการไม่เท่ากัน

ความสัมพันธ์ในระบบจำนวนจริง

  1. ถ้า a < b = b < c แล้ว จะได้ a < c

  2. ถ้า a < b แล้ว (a + c) < (b + c)

  3. ถ้า a < b แล้ว (a x c) < (b x c) ; c จะต้องเป็นค่าบวก

  4. ถ้า a < b แล้ว (a x c) > (b x c) ; c จะต้องเป็นค่าลบ

  5. ถ้า a < b แล้ว (a / c) < (b / c) ; c จะต้องเป็นค่าบวก

  6. ถ้า a < b แล้ว (a / c) > (b / c) ; c จะต้องเป็นค่าลบ

  7.          เว้นแต่ a = 0

a^{2}<0

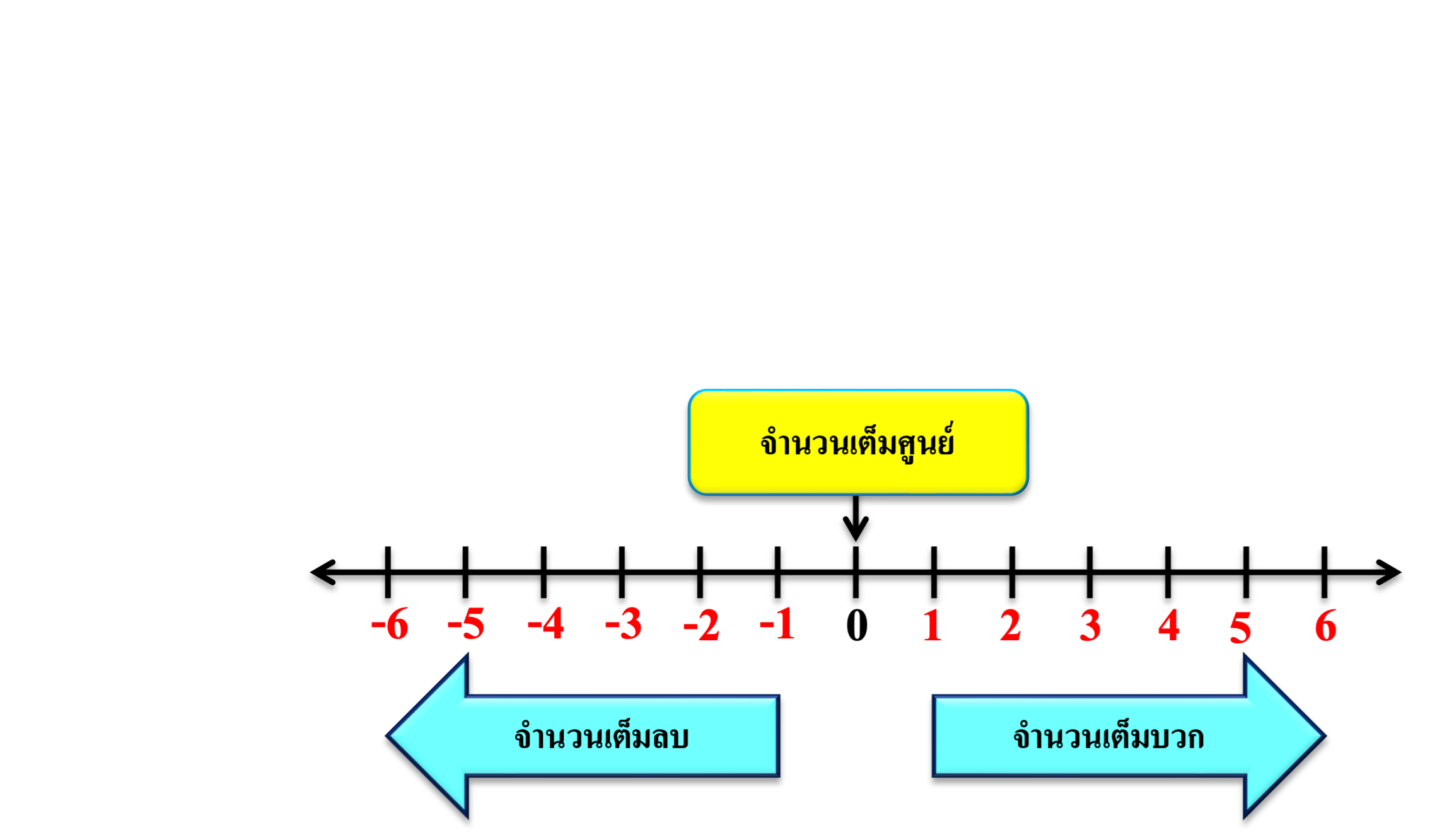
เส้นจำนวน

ช่วงของจำนวนจริง

จำนวนจริงทุกจำนวนระหว่าง a ถึง b

a

b

จำนวนจริงทุกจำนวนระหว่าง a ถึง b ไม่รวม a และ b

a

b

เส้นจำนวน

ช่วงของจำนวนจริง

จำนวนจริงทุกจำนวนระหว่าง a ถึง b ไม่รวม a

จำนวนจริงทุกจำนวนระหว่าง a ถึง b ไม่รวม b

a

b

a

b

เส้นจำนวน

ช่วงของจำนวนจริง

จำนวนจริงทุกจำนวนระหว่าง a ถึงไม่สิ้นสุด (>= a)

จำนวนจริงทุกจำนวนระหว่างติดลบไม่สิ้นสุด ถึง b ไม่รวม b (< b)

a

b

a

b

เส้นจำนวน

ช่วงของจำนวนจริง

จำนวนจริงทุกจำนวนระหว่าง a ถึงไม่สิ้นสุด (>= a)

จำนวนจริงทุกจำนวนระหว่างติดลบไม่สิ้นสุด ถึง b (<= b)

a

b

a

b

การใช้ เครื่องหมาย/สัญญลักษณ์

สัญญลักษณ์ทางคณิตศาสตร์

  1. (a, b) จำนวน a ถึง b แต่ไม่รวม a และ b

  2. [a, b] จำนวน a ถึง b

  3. [a, b) จำนวน a ถึง b รวม a

  4. (a, b] จำนวน a ถึง b รวม b

  5.     สัญญลักษณ์ ไม่สิ้นสุด (Infinity) ทางด้านบวก

  6.       สัญญลักษณ์ ไม่สิ้นสุด (Infinity) ทางด้านติดลบ

  7.     มากกว่า                     มากกว่าหรือเท่ากับ

  8.     น้อยกว่า                    น้อยกว่าหรือเท่ากับ

\infty
-\infty
>
\geqslant
<
\leqslant

Aj. Krit Th.

https://www.kritth.com